We  extensively investigated instabilities in 2D  periodic structures. We demonstrated that microscopic instabilities in 2D periodic porous structures at the millimeter scale result in dramatic transformations of the original geometry. As a result of a microscopic instability a square array of circular holes in an elastomeric matrix is found, upon reaching a critical applied stress, to suddenly transform to a periodic pattern of alternating, mutually orthogonal, ellipses. Differently, an oblique array of circular holes transforms into one of sheared voids where the shear direction alternates back and forth from row to row. Finally a rectangular array of elliptical holes is observed to transform to alternating arrays of high and low aspect ratio ellipses.

Examples of pattern switches in 2D periodic porous structures subjected to uniaxial loading as indicated by the orange arrows; the blue arrow points on the post-buckling configuration.

For elastic materials the geometric reorganization occurring at the onset of instability is both reversible and repeatable and occurs over a narrow range of the applied load. Thus this behavior provides opportunities for materials with properties that can switch in a sudden, but controlled manner.

The design problem of identifying periodic topologies where buckling can be exploited to tune the material functionalities is not trivial and requires robust algorithms. Initially we only used intuition  to design such 2D systems. As a result, only a limited number of pore arrangements (i.e. square and triangular arrays of holes) and shapes (i.e circular and elliptical holes) have been investigated. Recently,  we investigated the hole arrangements by considering geometric constraints on the tilings (i.e. tessellations) of the 2D Euclidean plan and identified all possible periodic distribution of mono-disperse circular holes where buckling leads to closure of all pores and enhanced compaction. We found that only four configurations exist where buckling leads to a periodic pattern of elongated ellipses with reduced symmetry. While two of these four configurations have been previously reported, the other two are newly discovered. Remarkably, in these two new configurations elastic buckling acts also as a reversible chiral symmetry-breaking mechanism, enabling a switch between  achiral and chiral patterns.  Moreover, since the proposed folding mechanism exploits a mechanical instability in elastic structures, our study opens avenues for the design of foldable materials over a wide range of length scales.

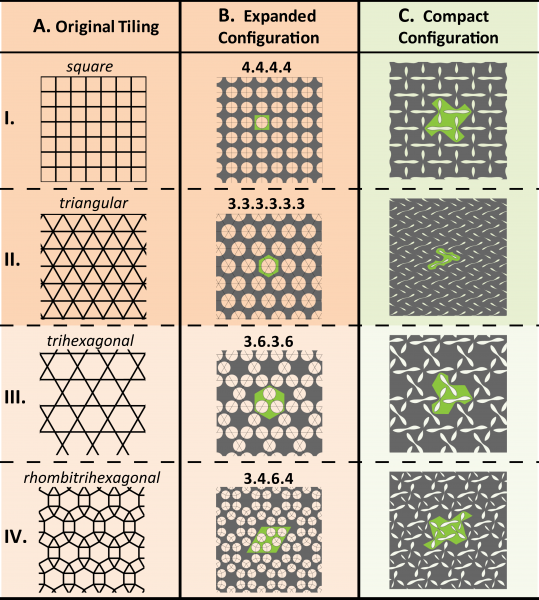
Geometric compatibility for the arrangement of circular holes on the porous structures, restricted to four specific configurations (shown in each row). (A) Tilings. (B) Expanded undeformed porous structures. (C) Compact porous structures, which are buckled under uniaxial compression. The green-shaded regions in (B) and (C) denote the unit cell in the undeformed and deformed configurations, respectively.

We also discovered pattern transformations induced by instabilities in 2D granular crystals (i.e. 2D ordered arrays of particles). The results of our experimental and numerical study demonstrated a pattern transformation in a regular array of millimeter-scale cylindrical particles with contrasting dimensions and softness. Under uniaxial compression the system undergoes a rearrangement which leads to a new periodic pattern. The details of the transformation process depend on the size ratio of the constituent particles but the final state after compression is robust. At small ratios it is homogeneous and approximately reversible, i.e. the initial geometry is almost recovered after unloading. In contrast, when the size ratio is increased the same final pattern is reached but now involves the sudden rearrangement of the particles via the formation of a shear band. The robustness of the experimental results and the scalability of the numerical work suggests a way of creating novel soft solids with interesting acoustic and optical properties.

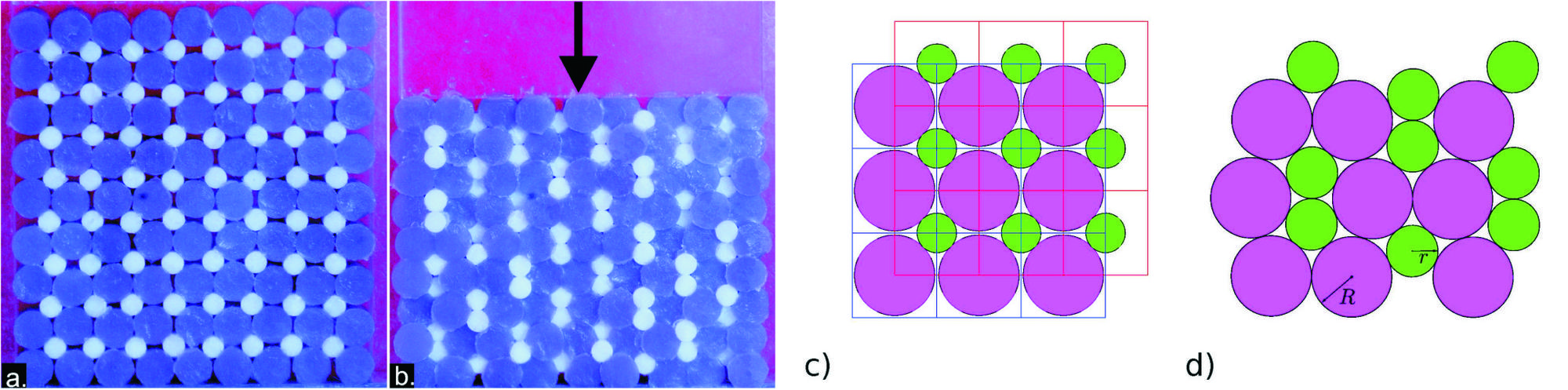
(a) Initial configuration of the 2D granular crystal. (b) Deformed configuration of the crystal at 30\% uniaxial compression. (c) The initial structure of the crystal consists of two embedded square lattices for small and large particles. (d) The final pattern consists of a vertically aligned pair of small particles surrounded by 6 large ones.

Publications:

• J. Shim, S. Shan, A. Kosmrlj, S.H. Kang, E.R. Chen, and K. Bertoldi. A complete class od 2D porous architectures where buckling leads to compaction. Soft Matter, 2013
• F. Goncu, S. Willshaw, J. Shim, J. Cusack, S. Luding, T. Mullin and K. Bertoldi. Deformation induced pattern transformation in a soft granular crystal. Soft Matter, 7: 2321-2324, 2011.